How to perfectly slice pizza, according to science

Two academics have discovered how to carve up pizza equally - to infinity

(2014 AFP)

Dividing up hot pizza equally usually means a frustrating wait, inevitable failure and someone making do with a disappointing sliver.

If only science had the answer, thought two mathematicians at the University of Liverpool.

So they set out to find it. Joel Haddley and Stephen Worsley’s new paper on the topic builds on existing circular geometry research, which recommends monohedrally tiling your pizza. Simply put, previous mathematicians had advised carving three wavy lines through the centre of your pizza, to make six pieces like this. These pieces can then be equally subdivided into 12, and so on.

How previous research recommended slicing your pizza: cut three wavy lines to make six equal slices, which can be subdivided again (University of Liverpool)

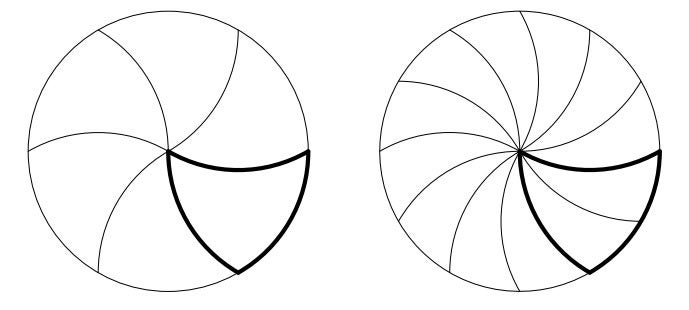
But Haddley and Worsley’s new technique proves that, as long as you cut your pizza into scythe-shaped, curved slices with an odd-number of sides – known as 5-gons, 7-gons, 9-gons and so on – each of those slices can continue being equally subdivided to infinity.

The perfect slicing pattern for an infinite number of equally-sized pizza slices, according to mathematicians Joel Haddley and Stephen Worsley (University of Liverpool)

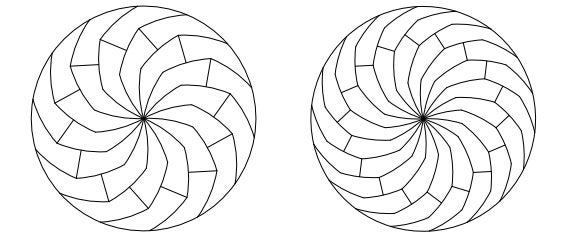
“Mathematically, there is no limit whatsoever,” Haddley told New Scientist. Your knife skills and your guests’ appetites however, may intervene to stop you monohedrally tiling your pizza to your heart's content.

“I’ve no idea whether there are any applications at all to our work outside of pizza-cutting,” Haddley said, but “you can produce some nice pictures.”

You can even add extra notches for intricacy, if your pizza getting cold is of no concern.

Monohedral pizza slices, with notches (University of Liverpool)

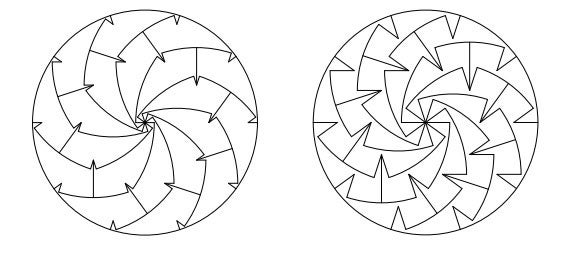
One advantage of the new technique is that crust is divided unequally, meaning crust haters can choose slices from the centre, while crust lovers can pick slices from the rim.

Just make sure you invite an equal number of pro and anti-crust eaters to your pizza party – and no word yet from the mathematicians on how to guarantee this.